Digital Circuits - Conversion of Flip-Flops

In previous chapter, we discussed the four flip-flops, namely SR flip-flop, D flip-flop, JK flip-flop & T flip-flop. We can convert one flip-flop into the remaining three flip-flops by including some additional logic. So, there will be total of twelve flip-flop conversions.

Follow these steps for converting one flip-flop to the other.

Consider the characteristic table of desired flip-flop.
Fill the excitation values (inputs) of given flip-flop for each combination of present state and next state. The excitation table for all flip-flops is shown below.

Present State	Next State	SR flip-flop inputs		D flip-flop input	JK flip-flop inputs		T flip-flop input
Q(t)	Q(t+1)	S	R	D	J	K	T
0	0	0	x	0	0	x	0
0	1	1	0	1	1	x	1
1	0	0	1	0	x	1	1
1	1	x	0	1	x	0	0

Get the simplified expressions for each excitation input. If necessary, use Kmaps for simplifying.
Draw the circuit diagram of desired flip-flop according to the simplified expressions using given flip-flop and necessary logic gates.

Now, let us convert few flip-flops into other. Follow the same process for remaining flipflop conversions.

SR Flip-Flop to other Flip-Flop Conversions

Following are the three possible conversions of SR flip-flop to other flip-flops.

SR flip-flop to D flip-flop
SR flip-flop to JK flip-flop
SR flip-flop to T flip-flop

SR flip-flop to D flip-flop conversion

Here, the given flip-flop is SR flip-flop and the desired flip-flop is D flip-flop. Therefore, consider the following characteristic table of D flip-flop.

D flip-flop input	Present State	Next State
D	Q(t)	Q(t + 1)
0	0	0
0	1	0
1	0	1
1	1	1

We know that SR flip-flop has two inputs S & R. So, write down the excitation values of SR flip-flop for each combination of present state and next state values. The following table shows the characteristic table of D flip-flop along with the excitation inputs of SR flip-flop.

D flip-flop input	Present State	Next State	SR flip-flop inputs
D	Q(t)	Q(t + 1)	S	R
0	0	0	0	x
0	1	0	0	1
1	0	1	1	0
1	1	1	x	0

From the above table, we can write the Boolean functions for each input as below.

S = m_{2} + d_{3}

R = m_{1} + d_{0}

We can use 2 variable K-Maps for getting simplified expressions for these inputs. The k-Maps for S & R are shown below.

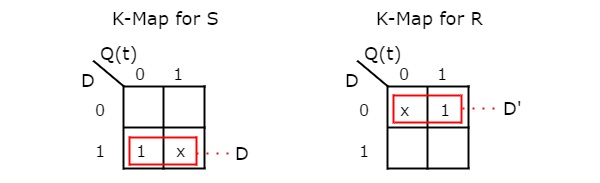
So, we got S = D & R = D' after simplifying. The circuit diagram of D flip-flop is shown in the following figure.

This circuit consists of SR flip-flop and an inverter. This inverter produces an output, which is complement of input, D. So, the overall circuit has single input, D and two outputs Q(t) & Q(t)'. Hence, it is a D flip-flop. Similarly, you can do other two conversions.

D Flip-Flop to other Flip-Flop Conversions

Following are the three possible conversions of D flip-flop to other flip-flops.

D flip-flop to T flip-flop
D flip-flop to SR flip-flop
D flip-flop to JK flip-flop

D flip-flop to T flip-flop conversion

Here, the given flip-flop is D flip-flop and the desired flip-flop is T flip-flop. Therefore, consider the following characteristic table of T flip-flop.

T flip-flop input	Present State	Next State
T	Q(t)	Q(t + 1)
0	0	0
0	1	1
1	0	1
1	1	0

We know that D flip-flop has single input D. So, write down the excitation values of D flip-flop for each combination of present state and next state values. The following table shows the characteristic table of T flip-flop along with the excitation input of D flip-flop.

T flip-flop input	Present State	Next State	D flip-flop input
T	Q(t)	Q(t + 1)	D
0	0	0	0
0	1	1	1
1	0	1	1
1	1	0	0

From the above table, we can directly write the Boolean function of D as below.

D = T \oplus Q (t)

So, we require a two input Exclusive-OR gate along with D flip-flop. The circuit diagram of T flip-flop is shown in the following figure.

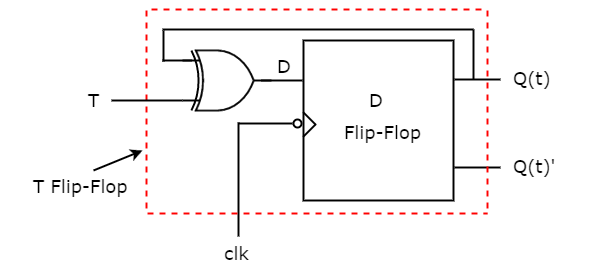
This circuit consists of D flip-flop and an Exclusive-OR gate. This Exclusive-OR gate produces an output, which is Ex-OR of T and Q(t). So, the overall circuit has single input, T and two outputs Q(t) & Q(t)’. Hence, it is a T flip-flop. Similarly, you can do other two conversions.

JK Flip-Flop to other Flip-Flop Conversions

Following are the three possible conversions of JK flip-flop to other flip-flops.

JK flip-flop to T flip-flop
JK flip-flop to D flip-flop
JK flip-flop to SR flip-flop

JK flip-flop to T flip-flop conversion

Here, the given flip-flop is JK flip-flop and the desired flip-flop is T flip-flop. Therefore, consider the following characteristic table of T flip-flop.

T flip-flop input	Present State	Next State
T	Q(t)	Q(t + 1)
0	0	0
0	1	1
1	0	1
1	1	0

We know that JK flip-flop has two inputs J & K. So, write down the excitation values of JK flip-flop for each combination of present state and next state values. The following table shows the characteristic table of T flip-flop along with the excitation inputs of JK flipflop.

T flip-flop input	Present State	Next State	JK flip-flop inputs
T	Q(t)	Q(t + 1)	J	K
0	0	0	0	x
0	1	1	x	0
1	0	1	1	x
1	1	0	x	1

From the above table, we can write the Boolean functions for each input as below.

J = m_{2} + d_{1} + d_{3}

K = m_{3} + d_{0} + d_{2}

We can use 2 variable K-Maps for getting simplified expressions for these two inputs. The k-Maps for J & K are shown below.

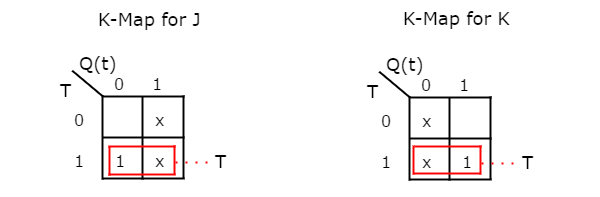
So, we got, J = T & K = T after simplifying. The circuit diagram of T flip-flop is shown in the following figure.

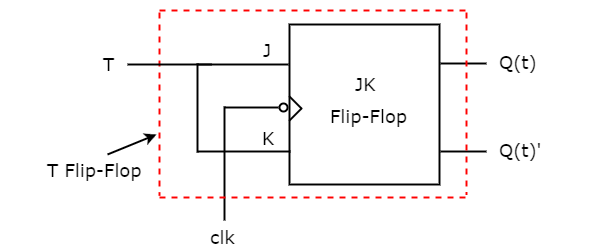
Circuit Diagram of T Flip-Flop with JK Flip-Flop

This circuit consists of JK flip-flop only. It doesn’t require any other gates. Just connect the same input T to both J & K. So, the overall circuit has single input, T and two outputs Q(t) & Q(t)’. Hence, it is a T flip-flop. Similarly, you can do other two conversions.

T Flip-Flop to other Flip-Flop Conversions

Following are the three possible conversions of T flip-flop to other flip-flops.

T flip-flop to D flip-flop
T flip-flop to SR flip-flop
T flip-flop to JK flip-flop

T flip-flop to D flip-flop conversion

Here, the given flip-flop is T flip-flop and the desired flip-flop is D flip-flop. Therefore, consider the characteristic table of D flip-flop and write down the excitation values of T flip-flop for each combination of present state and next state values. The following table shows the characteristic table of D flip-flop along with the excitation input of T flip-flop.

D flip-flop input	Present State	Next State	T flip-flop input
D	Q(t)	Q(t + 1)	T
0	0	0	0
0	1	0	1
1	0	1	1
1	1	1	0

From the above table, we can directly write the Boolean function of T as below.

T = D \oplus Q (t)

So, we require a two input Exclusive-OR gate along with T flip-flop. The circuit diagram of D flip-flop is shown in the following figure.

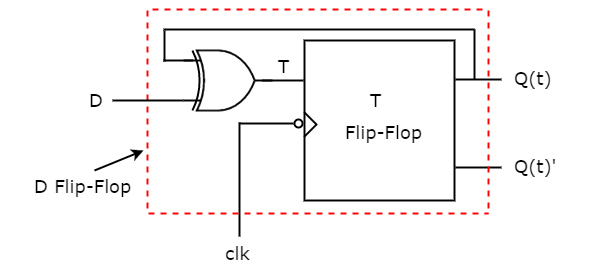
This circuit consists of T flip-flop and an Exclusive-OR gate. This Exclusive-OR gate produces an output, which is Ex-OR of D and Q(t). So, the overall circuit has single input, D and two outputs Q(t) & Q(t)’. Hence, it is a D flip-flop. Similarly, you can do other two conversions.

Discrete Mathematics - Rules of Inference

To deduce new statements from the statements whose truth that we already know, Rules of Inference are used. What are Rules of Inference for? Mathematical logic is often used for logical proofs. Proofs are valid arguments that determine the truth values of mathematical statements. An argument is a sequence of statements. The last statement is the conclusion and all its preceding statements are called premises (or hypothesis). The symbol “ ∴ ∴ ”, (read therefore) is placed before the conclusion. A valid argument is one where the conclusion follows from the truth values of the premises. Rules of Inference provide the templates or guidelines for constructing valid arguments from the statements that we already have. Table of Rules of Inference Rule of Inference Name Rule of Inference Name P ∴ P ∨ Q P ∴ P ∨ Q Addition P ∨ Q ¬ P ∴ Q P ∨ Q ¬ P ∴ Q Disjunctive Syllogism P Q ∴ P ∧ Q P Q ∴ P ∧ Q Conjunction P → Q Q → R ∴ P → R P → Q Q → R ∴ P → R ...

My skill

Search This Blog