discrete mathematics: Venn Diagrams

Venn Diagrams

Venn diagram, invented in 1880 by John Venn, is a schematic diagram that shows all possible logical relations between different mathematical sets.

Examples

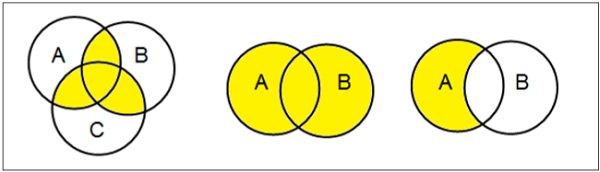
Set Operations

Set Operations include Set Union, Set Intersection, Set Difference, Complement of Set, and Cartesian Product.

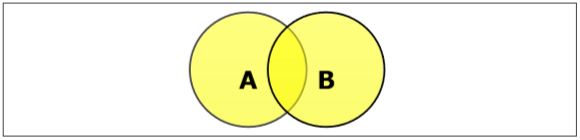
Set Union

The union of sets A and B (denoted by

A \cup B

) is the set of elements which are in A, in B, or in both A and B. Hence,

A \cup B = {x | x \in A O R x \in B}

Example − If

A = {10, 11, 12, 13}

and B =

{13, 14, 15}

, then

A \cup B = {10, 11, 12, 13, 14, 15}

. (The common element occurs only once)

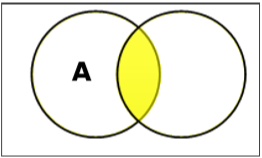
Set Intersection

The intersection of sets A and B (denoted by

A \cap B

) is the set of elements which are in both A and B. Hence,

A \cap B = {x | x \in A A N D x \in B}

Example − If

A = {11, 12, 13}

and

B = {13, 14, 15}

, then

A \cap B = {13}

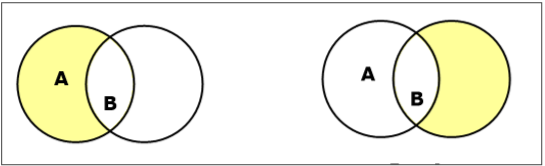
Set Difference/ Relative Complement

The set difference of sets A and B (denoted by

A - B

) is the set of elements which are only in A but not in B. Hence,

A - B = {x | x \in A A N D x \notin B}

Example − If

A = {10, 11, 12, 13}

and

B = {13, 14, 15}

, then

(A - B) = {10, 11, 12}

and

(B - A) = {14, 15}

. Here, we can see

(A - B) \neq (B - A)

Complement of a Set

The complement of a set A (denoted by

A^{'}

) is the set of elements which are not in set A. Hence,

A^{'} = {x | x \notin A}

More specifically,

A^{'} = (U - A)

where

U

is a universal set which contains all objects.

Example − If

A = {x | x b e l o n g s t o s e t o f o d d i n t e g e r s}

then

A^{'} = {y | y d o e s n o t b e l o n g t o s e t o f o d d i n t e g e r s}

Cartesian Product / Cross Product

The Cartesian product of n number of sets

A_{1}, A_{2}, \dots A_{n}

denoted as

A_{1} \times A_{2} \dots \times A_{n}

can be defined as all possible ordered pairs

(x_{1}, x_{2}, \dots x_{n})

where

x_{1} \in A_{1}, x_{2} \in A_{2}, \dots x_{n} \in A_{n}

Example − If we take two sets

A = {a, b}

and

B = {1, 2}

The Cartesian product of A and B is written as −

A \times B = {(a, 1), (a, 2), (b, 1), (b, 2)}

The Cartesian product of B and A is written as −

B \times A = {(1, a), (1, b), (2, a), (2, b)}

Power Set

Power set of a set S is the set of all subsets of S including the empty set. The cardinality of a power set of a set S of cardinality n is

2^{n}

. Power set is denoted as

P (S)

Example −

For a set

S = {a, b, c, d}

let us calculate the subsets −

Subsets with 0 elements − ${\emptyset}$ (the empty set)
Subsets with 1 element − ${a}, {b}, {c}, {d}$
Subsets with 2 elements − ${a, b}, {a, c}, {a, d}, {b, c}, {b, d}, {c, d}$
Subsets with 3 elements − ${a, b, c}, {a, b, d}, {a, c, d}, {b, c, d}$
Subsets with 4 elements − ${a, b, c, d}$

Hence,

P (S) =

{{\emptyset}, {a}, {b}, {c}, {d}, {a, b}, {a, c}, {a, d}, {b, c}, {b, d}, {c, d}, {a, b, c}, {a, b, d}, {a, c, d}, {b, c, d}, {a, b, c, d}}

| P (S) | = 2^{4} = 16

Note − The power set of an empty set is also an empty set.

| P ({\emptyset}) | = 2^{0} = 1

Partitioning of a Set

Partition of a set, say S, is a collection of n disjoint subsets, say

P_{1}, P_{2}, \dots P_{n}

that satisfies the following three conditions −

$P_{i}$ does not contain the empty set.

$[P_{i} \neq {\emptyset} f o r a l l 0 < i \leq n]$
The union of the subsets must equal the entire original set.

$[P_{1} \cup P_{2} \cup \dots \cup P_{n} = S]$
The intersection of any two distinct sets is empty.

$[P_{a} \cap P_{b} = {\emptyset}, f o r a \neq b w h e r e n \geq a, b \geq 0]$

Example

Let

S = {a, b, c, d, e, f, g, h}

One probable partitioning is

{a}, {b, c, d}, {e, f, g, h}

Another probable partitioning is

{a, b}, {c, d}, {e, f, g, h}

Bell Numbers

Bell numbers give the count of the number of ways to partition a set. They are denoted by

B_{n}

where n is the cardinality of the set.

Example −

Let

S = {1, 2, 3}

n = | S | = 3

The alternate partitions are −

\emptyset, {1, 2, 3}

{1}, {2, 3}

{1, 2}, {3}

{1, 3}, {2}

{1}, {2}, {3}

Hence

B_{3} = 5

My skill

Search This Blog