Discrete Mathematics - Relations

Whenever sets are being discussed, the relationship between the elements of the sets is the next thing that comes up. Relations may exist between objects of the same set or between objects of two or more sets.

Definition and Properties

A binary relation R from set x to y (written as xRy$xRy$ or R(x,y)$R(x,y)$) is a subset of the Cartesian product x×y$x\times y$. If the ordered pair of G is reversed, the relation also changes.

Generally an n-ary relation R between sets A1,…, and An$A_1,\dots ,and{A}_n$ is a subset of the n-ary product A1×⋯×An$A_1\times \cdots \times A_n$. The minimum cardinality of a relation R is Zero and maximum is n2$n^2$ in this case.

A binary relation R on a single set A is a subset of A×A$A\times A$.

For two distinct sets, A and B, having cardinalities m and n respectively, the maximum cardinality of a relation R from A to B is mn.

Domain and Range

If there are two sets A and B, and relation R have order pair (x, y), then −

• The domain of R, Dom(R), is the set {x|(x,y)∈RforsomeyinB}$\{x|(x,y)\in RforsomeyinB\}$
• The range of R, Ran(R), is the set {y|(x,y)∈RforsomexinA}$\{y|(x,y)\in RforsomexinA\}$

Examples

Let, A={1,2,9}$A=\{1,2,9\}$ and B={1,3,7}$B=\{1,3,7\}$

• Case 1 − If relation R is 'equal to' then R={(1,1),(3,3)}$R=\{(1,1),(3,3)\}$
  Dom(R) = {1,3},Ran(R)={1,3}$\{1,3\},Ran(R)=\{1,3\}$
• Case 2 − If relation R is 'less than' then R={(1,3),(1,7),(2,3),(2,7)}$R=\{(1,3),(1,7),(2,3),(2,7)\}$
  Dom(R) = {1,2},Ran(R)={3,7}$\{1,2\},Ran(R)=\{3,7\}$
• Case 3 − If relation R is 'greater than' then R={(2,1),(9,1),(9,3),(9,7)}$R=\{(2,1),(9,1),(9,3),(9,7)\}$
  Dom(R) = {2,9},Ran(R)={1,3,7}$\{2,9\},Ran(R)=\{1,3,7\}$

Representation of Relations using Graph

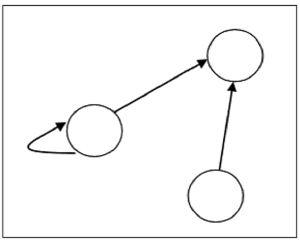
A relation can be represented using a directed graph.

The number of vertices in the graph is equal to the number of elements in the set from which the relation has been defined. For each ordered pair (x, y) in the relation R, there will be a directed edge from the vertex ‘x’ to vertex ‘y’. If there is an ordered pair (x, x), there will be self- loop on vertex ‘x’.

Suppose, there is a relation R={(1,1),(1,2),(3,2)}$R=\{(1,1),(1,2),(3,2)\}$ on set S={1,2,3}$S=\{1,2,3\}$, it can be represented by the following graph −

Types of Relations

• The Empty Relation between sets X and Y, or on E, is the empty set ∅$\mathrm{\varnothing }$
• The Full Relation between sets X and Y is the set X×Y$X\times Y$
• The Identity Relation on set X is the set {(x,x)|x∈X}$\{(x,x)|x\in X\}$
• The Inverse Relation R' of a relation R is defined as − R′={(b,a)|(a,b)∈R}$R^{\prime }=\{(b,a)|(a,b)\in R\}$
  Example − If R={(1,2),(2,3)}$R=\{(1,2),(2,3)\}$ then R′$R^{\prime }$ will be {(2,1),(3,2)}$\{(2,1),(3,2)\}$
• A relation R on set A is called Reflexive if ∀a∈A$\mathrm{\forall }a\in A$ is related to a (aRa holds)
  Example − The relation R={(a,a),(b,b)}$R=\{(a,a),(b,b)\}$ on set X={a,b}$X=\{a,b\}$ is reflexive.
• A relation R on set A is called Irreflexive if no a∈A$a\in A$ is related to a (aRa does not hold).
  Example − The relation R={(a,b),(b,a)}$R=\{(a,b),(b,a)\}$ on set X={a,b}$X=\{a,b\}$ is irreflexive.
• A relation R on set A is called Symmetric if xRy$xRy$ implies yRx$yRx$, ∀x∈A$\mathrm{\forall }x\in A$and ∀y∈A$\mathrm{\forall }y\in A$.
  Example − The relation R={(1,2),(2,1),(3,2),(2,3)}$R=\{(1,2),(2,1),(3,2),(2,3)\}$ on set A={1,2,3}$A=\{1,2,3\}$ is symmetric.
• A relation R on set A is called Anti-Symmetric if xRy$xRy$ and yRx$yRx$ impliesx=y∀x∈A$x=y\mathrm{\forall }x\in A$ and ∀y∈A$\mathrm{\forall }y\in A$.
  Example − The relation R={(x,y)→N|x≤y}$R=\{(x,y)\to N|x\le y\}$ is anti-symmetric since x≤y$x\le y$ and y≤x$y\le x$ implies x=y$x=y$.
• A relation R on set A is called Transitive if xRy$xRy$ and yRz$yRz$ implies xRz,∀x,y,z∈A$xRz,\mathrm{\forall }x,y,z\in A$.
  Example − The relation R={(1,2),(2,3),(1,3)}$R=\{(1,2),(2,3),(1,3)\}$ on set A={1,2,3}$A=\{1,2,3\}$is transitive.
• A relation is an Equivalence Relation if it is reflexive, symmetric, and transitive.
  Example − The relation R={(1,1),(2,2),(3,3),(1,2),(2,1),(2,3),(3,2),(1,3),(3,1)}$R=\{(1,1),(2,2),(3,3),(1,2),(2,1),(2,3),(3,2),(1,3),(3,1)\}$ on set A={1,2,3}$A=\{1,2,3\}$ is an equivalence relation since it is reflexive, symmetric, and transitive.