Skip to main content

Discrete Mathematics - Spanning Trees


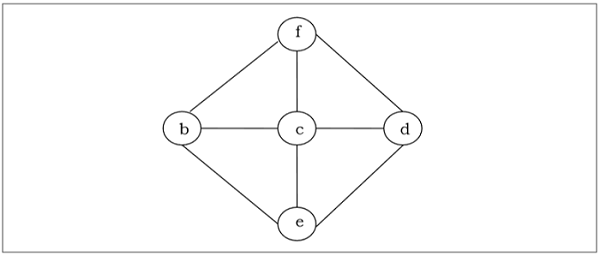
A spanning tree of a connected undirected graph G is a tree that minimally includes all of the vertices of G. A graph may have many spanning trees.

Example

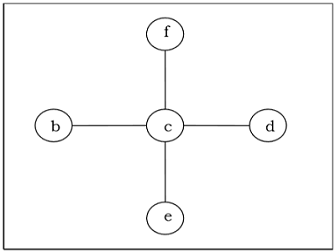
Graph in SpanSpanning Tree

Minimum Spanning Tree

A spanning tree with assigned weight less than or equal to the weight of every possible spanning tree of a weighted, connected and undirected graph G, it is called minimum spanning tree (MST). The weight of a spanning tree is the sum of all the weights assigned to each edge of the spanning tree.

Example

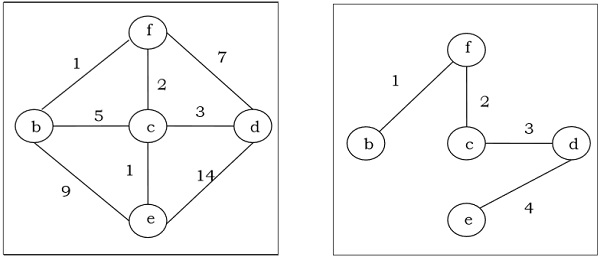
Minimum Spanning Tree

Kruskal's Algorithm

Kruskal's algorithm is a greedy algorithm that finds a minimum spanning tree for a connected weighted graph. It finds a tree of that graph which includes every vertex and the total weight of all the edges in the tree is less than or equal to every possible spanning tree.

Algorithm

Step 1 − Arrange all the edges of the given graph G(V,E) in non-decreasing order as per their edge weight.
Step 2 − Choose the smallest weighted edge from the graph and check if it forms a cycle with the spanning tree formed so far.
Step 3 − If there is no cycle, include this edge to the spanning tree else discard it.
Step 4 − Repeat Step 2 and Step 3 until (V−1) number of edges are left in the spanning tree.
Problem
Suppose we want to find minimum spanning tree for the following graph G using Kruskal’s algorithm.
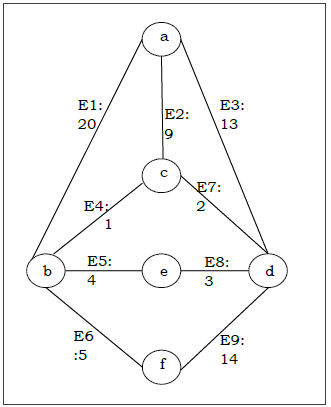
Kruskal Problem
Solution
From the above graph we construct the following table −
Edge No.Vertex PairEdge Weight
E1(a, b)20
E2(a, c)9
E3(a, d)13
E4(b, c)1
E5(b, e)4
E6(b, f)5
E7(c, d)2
E8(d, e)3
E9(d, f)14
Now we will rearrange the table in ascending order with respect to Edge weight −
Edge No.Vertex PairEdge Weight
E4(b, c)1
E7(c, d)2
E8(d, e)3
E5(b, e)4
E6(b, f)5
E2(a, c)9
E3(a, d)13
E9(d, f)14
E1(a, b)20
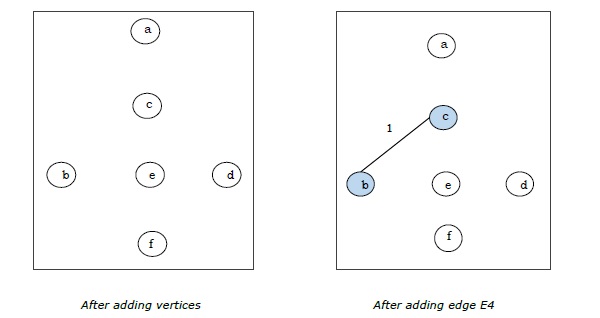
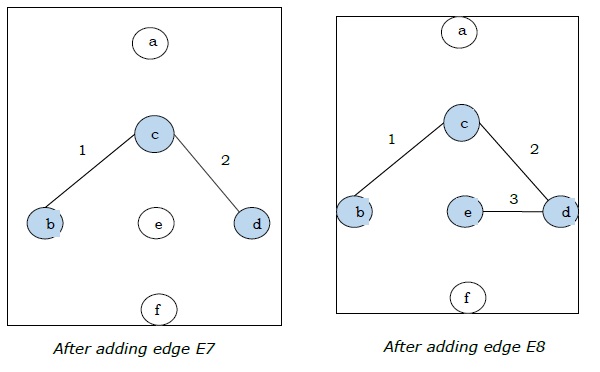
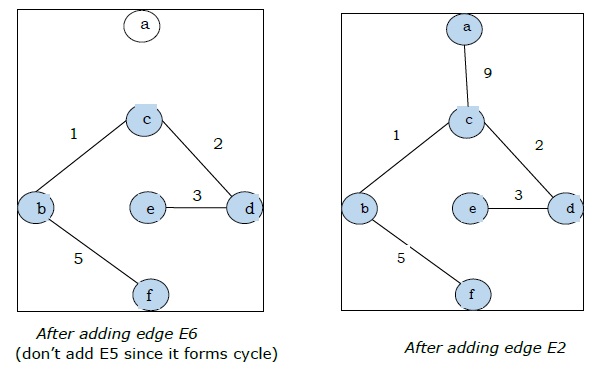
Kruskal Adding Vertex EdgeKruskal Adding Vertex Edge 1Kruskal Adding Vertex Edge 2
Since we got all the 5 edges in the last figure, we stop the algorithm and this is the minimal spanning tree and its total weight is (1+2+3+5+9)=20.

Prim's Algorithm

Prim's algorithm, discovered in 1930 by mathematicians, Vojtech Jarnik and Robert C. Prim, is a greedy algorithm that finds a minimum spanning tree for a connected weighted graph. It finds a tree of that graph which includes every vertex and the total weight of all the edges in the tree is less than or equal to every possible spanning tree. Prim’s algorithm is faster on dense graphs.

Algorithm

  • Initialize the minimal spanning tree with a single vertex, randomly chosen from the graph.
  • Repeat steps 3 and 4 until all the vertices are included in the tree.
  • Select an edge that connects the tree with a vertex not yet in the tree, so that the weight of the edge is minimal and inclusion of the edge does not form a cycle.
  • Add the selected edge and the vertex that it connects to the tree.
Problem
Suppose we want to find minimum spanning tree for the following graph G using Prim’s algorithm.
Prim
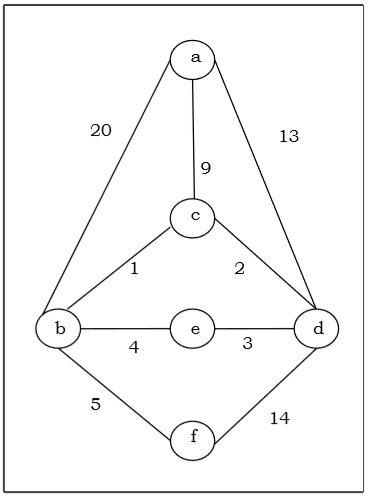
Solution
Here we start with the vertex ‘a’ and proceed.
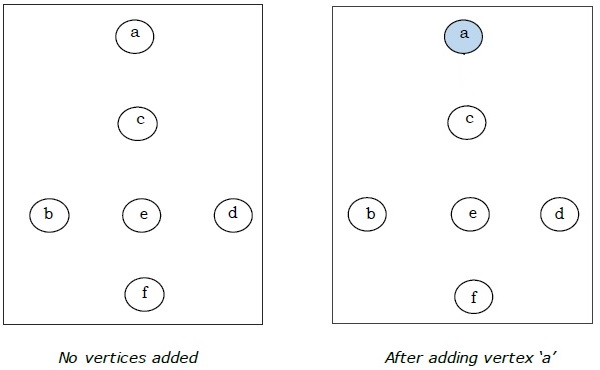
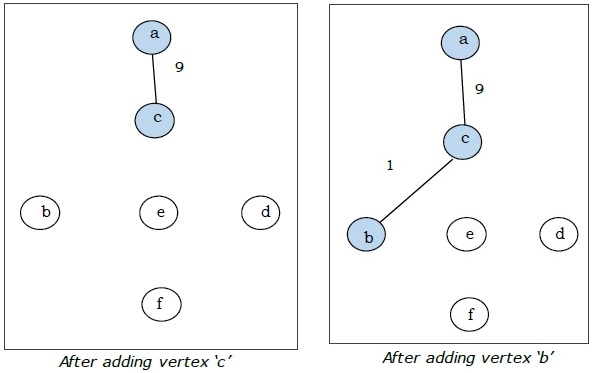
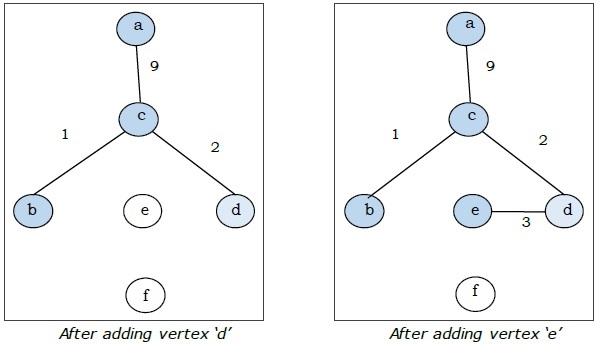
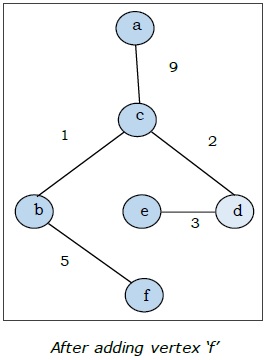
prim' Vertex a addedprim' Vertex c b addedprim' Vertex d e addedprim' Vertex f added
This is the minimal spanning tree and its total weight is (1+2+3+5+9)=20.

Comments

Post a Comment

Popular posts from this blog

Discrete Mathematics - Rules of Inference

To deduce new statements from the statements whose truth that we already know,  Rules of Inference  are used. What are Rules of Inference for? Mathematical logic is often used for logical proofs. Proofs are valid arguments that determine the truth values of mathematical statements. An argument is a sequence of statements. The last statement is the conclusion and all its preceding statements are called premises (or hypothesis). The symbol “ ∴ ∴ ”, (read therefore) is placed before the conclusion. A valid argument is one where the conclusion follows from the truth values of the premises. Rules of Inference provide the templates or guidelines for constructing valid arguments from the statements that we already have. Table of Rules of Inference Rule of Inference Name Rule of Inference Name P ∴ P ∨ Q P ∴ P ∨ Q Addition P ∨ Q ¬ P ∴ Q P ∨ Q ¬ P ∴ Q Disjunctive Syllogism P Q ∴ P ∧ Q P Q ∴ P ∧ Q Conjunction P → Q Q → R ∴ P → R P → Q Q → R ∴ P → R ...
Post a Comment
Read more

Digital Circuits - Shift Registers

We know that one flip-flop can store one-bit of information. In order to store multiple bits of information, we require multiple flip-flops. The group of flip-flops, which are used to hold (store) the binary data is known as  register . If the register is capable of shifting bits either towards right hand side or towards left hand side is known as  shift register . An ‘N’ bit shift register contains ‘N’ flip-flops. Following are the four types of shift registers based on applying inputs and accessing of outputs. Serial In − Serial Out shift register Serial In − Parallel Out shift register Parallel In − Serial Out shift register Parallel In − Parallel Out shift register Serial In − Serial Out (SISO) Shift Register The shift register, which allows serial input and produces serial output is known as Serial In – Serial Out  (SISO)  shift register. The  block diagram  of 3-bit SISO shift register is shown in the following figure. This block d...
Post a Comment
Read more

discrete mathematics: Venn Diagrams

Venn Diagrams Venn diagram, invented in 1880 by John Venn, is a schematic diagram that shows all possible logical relations between different mathematical sets. Examples Set Operations Set Operations include Set Union, Set Intersection, Set Difference, Complement of Set, and Cartesian Product. Set Union The union of sets A and B (denoted by  A ∪ B A ∪ B ) is the set of elements which are in A, in B, or in both A and B. Hence,  A ∪ B = { x | x ∈ A   O R   x ∈ B } A ∪ B = { x | x ∈ A   O R   x ∈ B } . Example  − If  A = { 10 , 11 , 12 , 13 } A = { 10 , 11 , 12 , 13 }  and B =  { 13 , 14 , 15 } { 13 , 14 , 15 } , then  A ∪ B = { 10 , 11 , 12 , 13 , 14 , 15 } A ∪ B = { 10 , 11 , 12 , 13 , 14 , 15 } . (The common element occurs only once) Set Intersection The intersection of sets A and B (denoted by  A ∩ B A ∩ B ) is the set of elements which are in both A and B. Hence,  A ∩ B = { x | x ∈ A   A N D...
Post a Comment
Read more