discrete mathematics:Introduction to Trees

Tree is a discrete structure that represents hierarchical relationships between individual elements or nodes. A tree in which a parent has no more than two children is called a binary tree.

Tree and its Properties

Definition − A Tree is a connected acyclic undirected graph. There is a unique path between every pair of vertices in G$G$. A tree with N number of vertices contains (N−1)$(N-1)$ number of edges. The vertex which is of 0 degree is called root of the tree. The vertex which is of 1 degree is called leaf node of the tree and the degree of an internal node is at least 2.

Example − The following is an example of a tree −

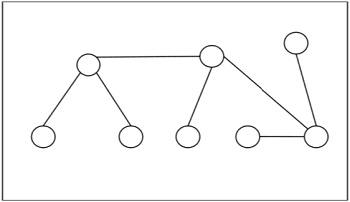
Centers and Bi-Centers of a Tree

The center of a tree is a vertex with minimal eccentricity. The eccentricity of a vertex X$X$ in a tree G$G$ is the maximum distance between the vertex X$X$ and any other vertex of the tree. The maximum eccentricity is the tree diameter. If a tree has only one center, it is called Central Tree and if a tree has only more than one centers, it is called Bi-central Tree. Every tree is either central or bi-central.

Algorithm to find centers and bi-centers of a tree

Step 1 − Remove all the vertices of degree 1 from the given tree and also remove their incident edges.

Step 2 − Repeat step 1 until either a single vertex or two vertices joined by an edge is left. If a single vertex is left then it is the center of the tree and if two vertices joined by an edge is left then it is the bi-center of the tree.

Problem 1

Find out the center/bi-center of the following tree −

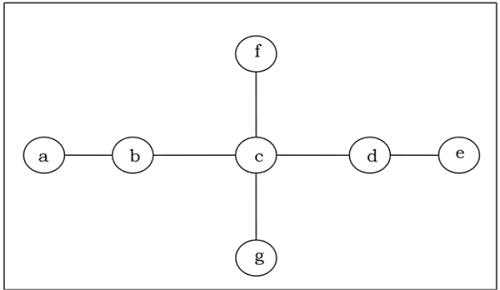
Solution

At first, we will remove all vertices of degree 1 and also remove their incident edges and get the following tree −

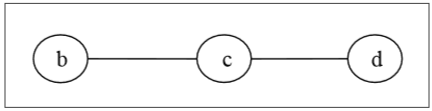
Again, we will remove all vertices of degree 1 and also remove their incident edges and get the following tree −

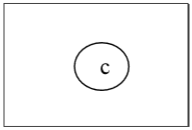
Finally we got a single vertex ‘c’ and we stop the algorithm. As there is single vertex, this tree has one center ‘c’ and the tree is a central tree.

Problem 2

Find out the center/bi-center of the following tree −

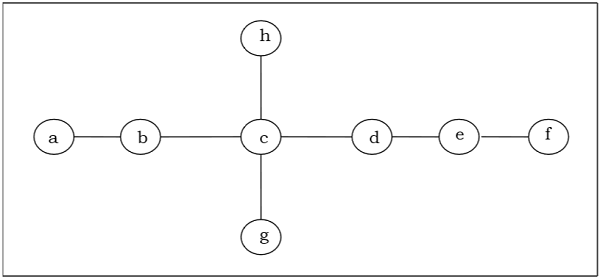
Solution

At first, we will remove all vertices of degree 1 and also remove their incident edges and get the following tree −

Again, we will remove all vertices of degree 1 and also remove their incident edges and get the following tree −

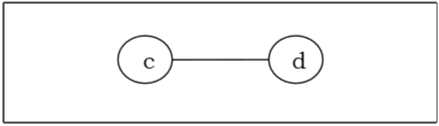
Finally, we got two vertices ‘c’ and ‘d’ left, hence we stop the algorithm. As two vertices joined by an edge is left, this tree has bi-center ‘cd’ and the tree is bi-central.

Labeled Trees

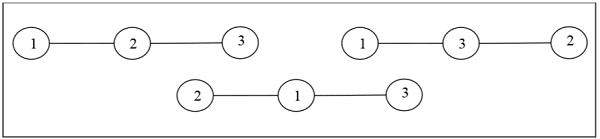
Definition − A labeled tree is a tree the vertices of which are assigned unique numbers from 1 to n. We can count such trees for small values of n by hand so as to conjecture a general formula. The number of labeled trees of n number of vertices is nn−2$n^{n-2}$. Two labeled trees are isomorphic if their graphs are isomorphic and the corresponding points of the two trees have the same labels.

Example

Unlabeled Trees

Definition − An unlabeled tree is a tree the vertices of which are not assigned any numbers. The number of labeled trees of n number of vertices is (2n)!(n+1)!n!$\frac{(2n)!}{(n+1)!n!}$(n^th Catalan number)

Example

Rooted Tree

A rooted tree G$G$ is a connected acyclic graph with a special node that is called the root of the tree and every edge directly or indirectly originates from the root. An ordered rooted tree is a rooted tree where the children of each internal vertex are ordered. If every internal vertex of a rooted tree has not more than m children, it is called an m-ary tree. If every internal vertex of a rooted tree has exactly m children, it is called a full m-ary tree. If m=2$m=2$, the rooted tree is called a binary tree.

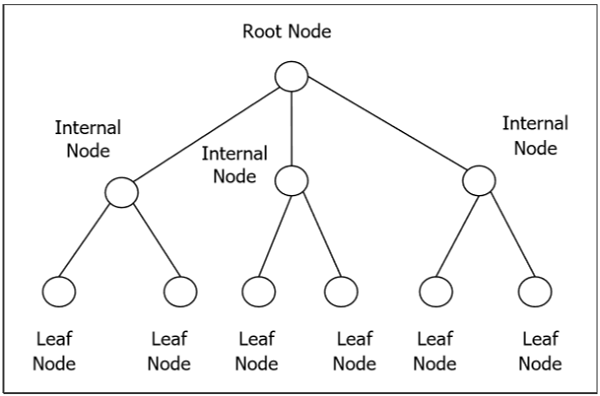
Binary Search Tree

Binary Search tree is a binary tree which satisfies the following property −

• X$X$ in left sub-tree of vertex V,Value(X)≤Value(V)$V,Value(X)\le Value(V)$
• Y$Y$ in right sub-tree of vertex V,Value(Y)≥Value(V)$V,Value(Y)\ge Value(V)$

So, the value of all the vertices of the left sub-tree of an internal node V$V$ are less than or equal to V$V$ and the value of all the vertices of the right sub-tree of the internal node V$V$ are greater than or equal to V$V$. The number of links from the root node to the deepest node is the height of the Binary Search Tree.

Example

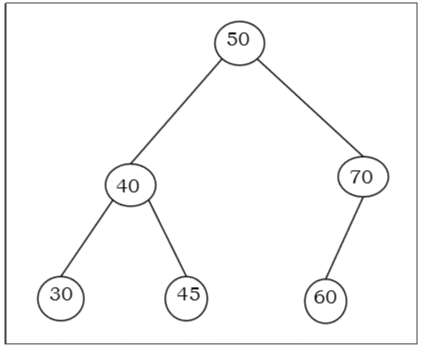
Algorithm to search for a key in BST

BST_Search(x, k) 
if ( x = NIL or k = Value[x] ) 
   return x; 
if ( k < Value[x]) 
   return BST_Search (left[x], k); 
else  
   return BST_Search (right[x], k)  

Complexity of Binary search tree

	Average Case	Worst case
Space Complexity	O(n)	O(n)
Search Complexity	O(log n)	O(n)
Insertion Complexity	O(log n)	O(n)
Deletion Complexity	O(log n)	O(n)