Simplification Of Boolean Functions

Simplification Using Algebraic Functions

In this approach, one Boolean expression is minimized into an equivalent expression by applying Boolean identities.

Problem 1

Minimize the following Boolean expression using Boolean identities −

F(A,B,C)=A′B+BC′+BC+AB′C′$$F(A,B,C)=A^{\prime }B+B{C}^{\prime }+BC+A{B}^{\prime }{C}^{\prime }$$

Solution

Given,F(A,B,C)=A′B+BC′+BC+AB′C′$F(A,B,C)=A^{\prime }B+B{C}^{\prime }+BC+A{B}^{\prime }{C}^{\prime }$

Or,F(A,B,C)=A′B+(BC′+BC′)+BC+AB′C′$F(A,B,C)=A^{\prime }B+(B{C}^{\prime }+B{C}^{\prime })+BC+A{B}^{\prime }{C}^{\prime }$

[By idempotent law, BC’ = BC’ + BC’]

Or,F(A,B,C)=A′B+(BC′+BC)+(BC′+AB′C′)$F(A,B,C)=A^{\prime }B+(B{C}^{\prime }+BC)+(B{C}^{\prime }+A{B}^{\prime }{C}^{\prime })$

Or,F(A,B,C)=A′B+B(C′+C)+C′(B+AB′)$F(A,B,C)=A^{\prime }B+B(C^{\prime }+C)+C^{\prime }(B+A{B}^{\prime })$

[By distributive laws]

Or,F(A,B,C)=A′B+B.1+C′(B+A)$F(A,B,C)=A^{\prime }B+B.1+C^{\prime }(B+A)$

[ (C' + C) = 1 and absorption law (B + AB')= (B + A)]

Or,F(A,B,C)=A′B+B+C′(B+A)$F(A,B,C)=A^{\prime }B+B+C^{\prime }(B+A)$

[ B.1 = B ]

Or,F(A,B,C)=B(A′+1)+C′(B+A)$F(A,B,C)=B(A^{\prime }+1)+C^{\prime }(B+A)$

Or,F(A,B,C)=B.1+C′(B+A)$F(A,B,C)=B.1+C^{\prime }(B+A)$

[ (A' + 1) = 1 ]

Or,F(A,B,C)=B+C′(B+A)$F(A,B,C)=B+C^{\prime }(B+A)$

[ As, B.1 = B ]

Or,F(A,B,C)=B+BC′+AC′$F(A,B,C)=B+B{C}^{\prime }+A{C}^{\prime }$

Or,F(A,B,C)=B(1+C′)+AC′$F(A,B,C)=B(1+C^{\prime })+A{C}^{\prime }$

Or,F(A,B,C)=B.1+AC′$F(A,B,C)=B.1+A{C}^{\prime }$

[As, (1 + C') = 1]

Or,F(A,B,C)=B+AC′$F(A,B,C)=B+A{C}^{\prime }$

[As, B.1 = B]

So,F(A,B,C)=B+AC′$F(A,B,C)=B+A{C}^{\prime }$is the minimized form.

Problem 2

Minimize the following Boolean expression using Boolean identities −

F(A,B,C)=(A+B)(B+C)$$F(A,B,C)=(A+B)(B+C)$$

Solution

Given, F(A,B,C)=(A+B)(A+C)$F(A,B,C)=(A+B)(A+C)$

Or, F(A,B,C)=A.A+A.C+B.A+B.C$F(A,B,C)=A.A+A.C+B.A+B.C$ [Applying distributive Rule]

Or, F(A,B,C)=A+A.C+B.A+B.C$F(A,B,C)=A+A.C+B.A+B.C$ [Applying Idempotent Law]

Or, F(A,B,C)=A(1+C)+B.A+B.C$F(A,B,C)=A(1+C)+B.A+B.C$ [Applying distributive Law]

Or, F(A,B,C)=A+B.A+B.C$F(A,B,C)=A+B.A+B.C$ [Applying dominance Law]

Or, F(A,B,C)=(A+1).A+B.C$F(A,B,C)=(A+1).A+B.C$ [Applying distributive Law]

Or, F(A,B,C)=1.A+B.C$F(A,B,C)=1.A+B.C$ [Applying dominance Law]

Or, F(A,B,C)=A+B.C$F(A,B,C)=A+B.C$ [Applying dominance Law]

So, F(A,B,C)=A+BC$F(A,B,C)=A+BC$ is the minimized form.

Karnaugh Maps

The Karnaugh map (K–map), introduced by Maurice Karnaughin in 1953, is a grid-like representation of a truth table which is used to simplify boolean algebra expressions. A Karnaugh map has zero and one entries at different positions. It provides grouping together Boolean expressions with common factors and eliminates unwanted variables from the expression. In a K-map, crossing a vertical or horizontal cell boundary is always a change of only one variable.

Example 1

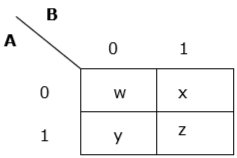
An arbitrary truth table is taken below −

A	B	A operation B
0	0	w
0	1	x
1	0	y
1	1	z

Now we will make a k-map for the above truth table −

Example 2

Now we will make a K-map for the expression − AB+ A’B’

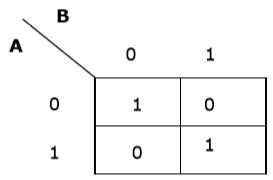
Simplification Using K-map

K-map uses some rules for the simplification of Boolean expressions by combining together adjacent cells into single term. The rules are described below −

Rule 1 − Any cell containing a zero cannot be grouped.

Wrong grouping

Rule 2 − Groups must contain 2n cells (n starting from 1).

Wrong grouping

Rule 3 − Grouping must be horizontal or vertical, but must not be diagonal.

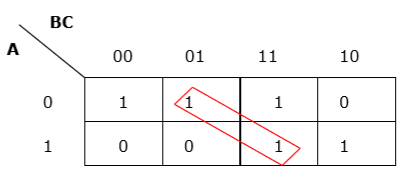
Wrong diagonal grouping

Proper vertical grouping

Proper horizontal grouping

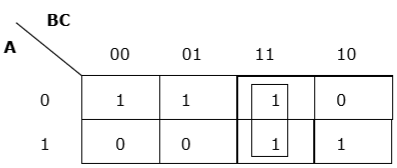
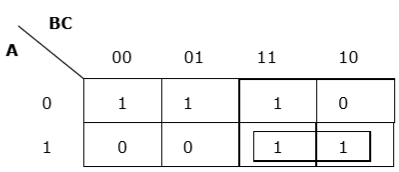
Rule 4 − Groups must be covered as largely as possible.

Insufficient grouping

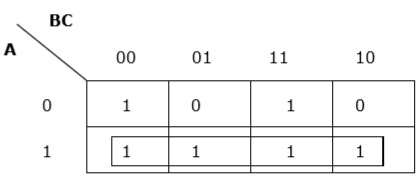
Proper grouping

Rule 5 − If 1 of any cell cannot be grouped with any other cell, it will act as a group itself.

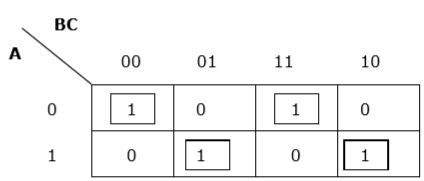
Proper grouping

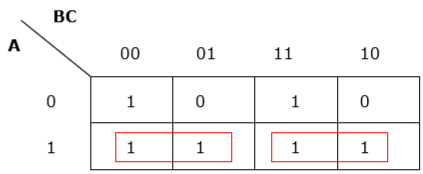
Rule 6 − Groups may overlap but there should be as few groups as possible.

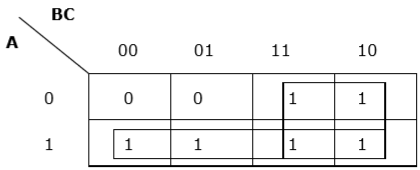
Proper grouping

Rule 7 − The leftmost cell/cells can be grouped with the rightmost cell/cells and the topmost cell/cells can be grouped with the bottommost cell/cells.

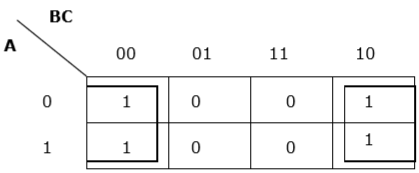
Proper grouping

Problem

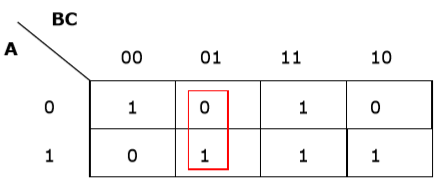
Minimize the following Boolean expression using K-map −

F(A,B,C)=A′BC+A′BC′+AB′C′+AB′C$$F(A,B,C)=A^{\prime }BC+A^{\prime }B{C}^{\prime }+A{B}^{\prime }{C}^{\prime }+A{B}^{\prime }C$$

Solution

Each term is put into k-map and we get the following −

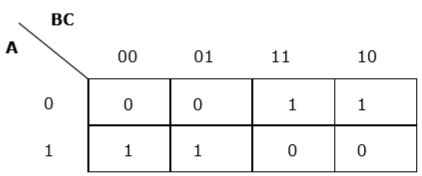
K-map for F (A, B, C)

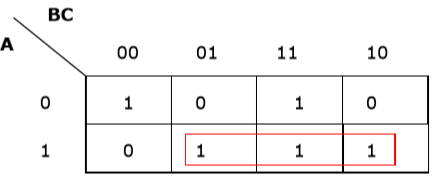
Now we will group the cells of 1 according to the rules stated above −

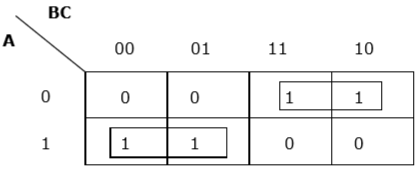
K-map for F (A, B, C)

We have got two groups which are termed as A′B$A^{\prime }B$ and AB′$A{B}^{\prime }$. Hence, F(A,B,C)=A′B+AB′=A⊕B$F(A,B,C)=A^{\prime }B+A{B}^{\prime }=A\oplus B$. It is the minimized form.