Skip to main content

Add Page Numbers in Word 2010


In this chapter, we will discuss how to add page numbers in Word 2010. Microsoft Word automatically assigns page numbers on the pages of your document. Typically, page numbers are printed either in header or footer but you have the option that can display the page number in the left or right margins at the top or the bottom of a page.

Add Page Numbers

Following are the simple steps to add page numbers in a Word document.
Step 1 − Click the Insert tab, and click the Page Number button available in the header and footer section. This will display a list of options to display the page number at the top, bottom, current position etc.
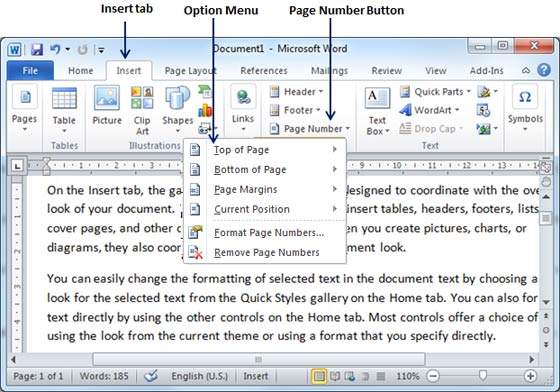
Page Number
Step 2 − When you move your mouse pointer over the available options, it displays further styles of page numbers to be displayed. For example, when I take the mouse pointer at the Bottom of Page option it displays the following list of styles.
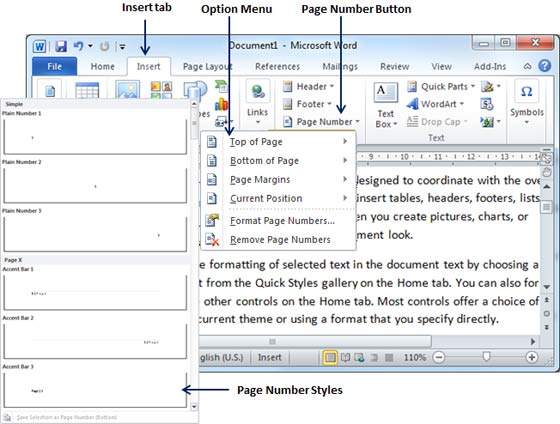
Page Number Styles
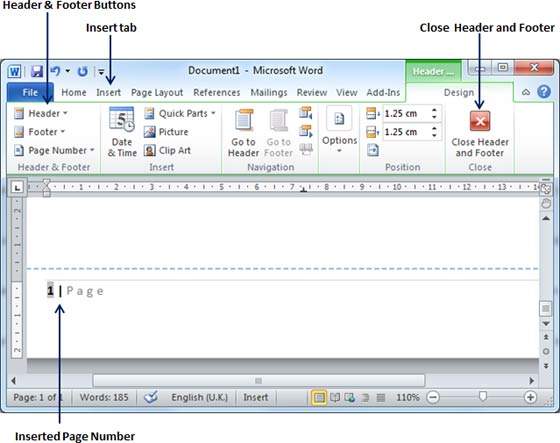
Step 3 − Finally, select any one of the page number styles. I selected the Accent Bar 1 style by clicking over it. You will be directed to the Page Footer modification mode. Click the Close Header and Footer button to come out of the Footer Edit mode.
You can format your page numbers using the Format Page Numbers option available under the listed options.
Inserted Page Number

Remove Page Numbers

The following steps will help you remove page numbering from a Word document.
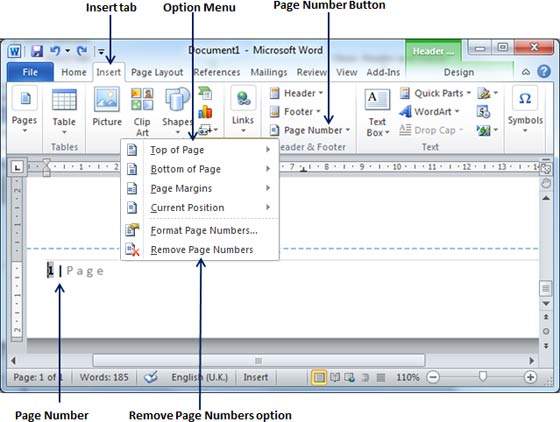
Step 1 − Click the Insert tab, and click the Page Number button available in the header and footer section. This will display a list of options to display page number at the top, bottom, current position, etc. At the bottom, you will have the Remove Page Numbers option. Just click this option and it will delete all the page numbers set in your document.
Remove Page Numbers

Labels

Labels:

Comments

Post a Comment

Popular posts from this blog

Discrete Mathematics - Rules of Inference

To deduce new statements from the statements whose truth that we already know,  Rules of Inference  are used. What are Rules of Inference for? Mathematical logic is often used for logical proofs. Proofs are valid arguments that determine the truth values of mathematical statements. An argument is a sequence of statements. The last statement is the conclusion and all its preceding statements are called premises (or hypothesis). The symbol “ ∴ ∴ ”, (read therefore) is placed before the conclusion. A valid argument is one where the conclusion follows from the truth values of the premises. Rules of Inference provide the templates or guidelines for constructing valid arguments from the statements that we already have. Table of Rules of Inference Rule of Inference Name Rule of Inference Name P ∴ P ∨ Q P ∴ P ∨ Q Addition P ∨ Q ¬ P ∴ Q P ∨ Q ¬ P ∴ Q Disjunctive Syllogism P Q ∴ P ∧ Q P Q ∴ P ∧ Q Conjunction P → Q Q → R ∴ P → R P → Q Q → R ∴ P → R ...
Post a Comment
Read more

5 best private search engines and why you need to use them.

5 best private search engines and why you need to use them  By:  Boniyeamin laju   ▪   May 31, 2019   ▪ 3 minute read 5 best private search engines and why you need to use  Normal browsers like Google and Bing are designed to track users’ activities and profile their online behavior. The primary reason for this is to create advertisements that will be attractive to the user. However, there-there is always the concern of  personal information being compromised  due to security breaches, state surveillance, and unauthorized data sharing. Fortunately,  private search engines  can help keep your private information safe. Simply put, Private Search Engines, also known as PSE, uses proxy and encrypted search request to  hide your personal information  from anyone looking to misuse your information. Below you will find more information about what a PSE is, how it works, and wh...
Post a Comment
Read more

discrete mathematics: Venn Diagrams

Venn Diagrams Venn diagram, invented in 1880 by John Venn, is a schematic diagram that shows all possible logical relations between different mathematical sets. Examples Set Operations Set Operations include Set Union, Set Intersection, Set Difference, Complement of Set, and Cartesian Product. Set Union The union of sets A and B (denoted by  A ∪ B A ∪ B ) is the set of elements which are in A, in B, or in both A and B. Hence,  A ∪ B = { x | x ∈ A   O R   x ∈ B } A ∪ B = { x | x ∈ A   O R   x ∈ B } . Example  − If  A = { 10 , 11 , 12 , 13 } A = { 10 , 11 , 12 , 13 }  and B =  { 13 , 14 , 15 } { 13 , 14 , 15 } , then  A ∪ B = { 10 , 11 , 12 , 13 , 14 , 15 } A ∪ B = { 10 , 11 , 12 , 13 , 14 , 15 } . (The common element occurs only once) Set Intersection The intersection of sets A and B (denoted by  A ∩ B A ∩ B ) is the set of elements which are in both A and B. Hence,  A ∩ B = { x | x ∈ A   A N D...
Post a Comment
Read more