An Encoder is a combinational circuit that performs the reverse operation of Decoder. It has maximum of 2n input lines and ‘n’ output lines. It will produce a binary code equivalent to the input, which is active High. Therefore, the encoder encodes 2n input lines with ‘n’ bits. It is optional to represent the enable signal in encoders.
4 to 2 Encoder
Let 4 to 2 Encoder has four inputs Y3, Y2, Y1 & Y0 and two outputs A1 & A0. The block diagram of 4 to 2 Encoder is shown in the following figure.
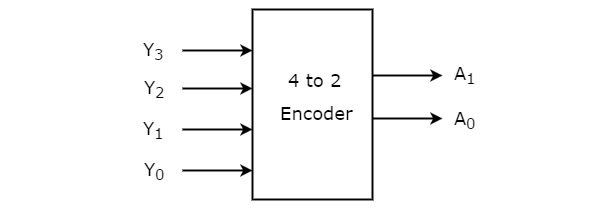
At any time, only one of these 4 inputs can be ‘1’ in order to get the respective binary code at the output. The Truth table of 4 to 2 encoder is shown below.
| Inputs | Outputs | ||||
|---|---|---|---|---|---|
| Y3 | Y2 | Y1 | Y0 | A1 | A0 |
| 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 | 1 |
From Truth table, we can write the Boolean functions for each output as
We can implement the above two Boolean functions by using two input OR gates. The circuit diagram of 4 to 2 encoder is shown in the following figure.
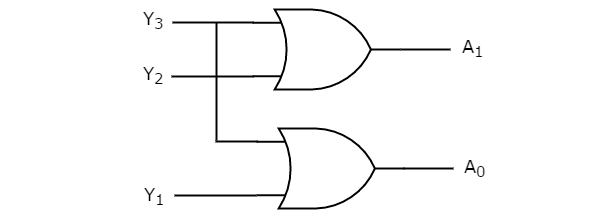
The above circuit diagram contains two OR gates. These OR gates encode the four inputs with two bits
Octal to Binary Encoder
Octal to binary Encoder has eight inputs, Y7 to Y0 and three outputs A2, A1 & A0. Octal to binary encoder is nothing but 8 to 3 encoder. The block diagram of octal to binary Encoder is shown in the following figure.
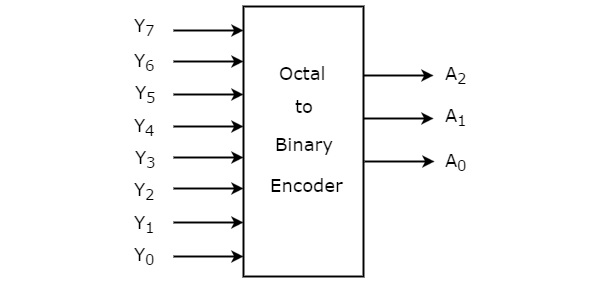
At any time, only one of these eight inputs can be ‘1’ in order to get the respective binary code. The Truth table of octal to binary encoder is shown below.
| Inputs | Outputs | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Y7 | Y6 | Y5 | Y4 | Y3 | Y2 | Y1 | Y0 | A2 | A1 | A0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
From Truth table, we can write the Boolean functions for each output as
We can implement the above Boolean functions by using four input OR gates. The circuit diagram of octal to binary encoder is shown in the following figure.
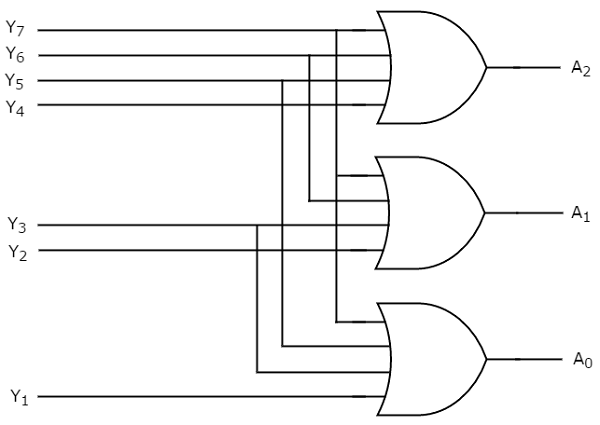
The above circuit diagram contains three 4-input OR gates. These OR gates encode the eight inputs with three bits.
Drawbacks of Encoder
Following are the drawbacks of normal encoder.
- There is an ambiguity, when all outputs of encoder are equal to zero. Because, it could be the code corresponding to the inputs, when only least significant input is one or when all inputs are zero.
- If more than one input is active High, then the encoder produces an output, which may not be the correct code. For example, if both Y3and Y6 are ‘1’, then the encoder produces 111 at the output. This is neither equivalent code corresponding to Y3, when it is ‘1’ nor the equivalent code corresponding to Y6, when it is ‘1’.
So, to overcome these difficulties, we should assign priorities to each input of encoder. Then, the output of encoder will be the (binary) code corresponding to the active High input(s), which has higher priority. This encoder is called as priority encoder.
Priority Encoder
A 4 to 2 priority encoder has four inputs Y3, Y2, Y1 & Y0 and two outputs A1 & A0. Here, the input, Y3 has the highest priority, whereas the input, Y0 has the lowest priority. In this case, even if more than one input is ‘1’ at the same time, the output will be the (binary) code corresponding to the input, which is having higher priority.
We considered one more output, V in order to know, whether the code available at outputs is valid or not.
- If at least one input of the encoder is ‘1’, then the code available at outputs is a valid one. In this case, the output, V will be equal to 1.
- If all the inputs of encoder are ‘0’, then the code available at outputs is not a valid one. In this case, the output, V will be equal to 0.
The Truth table of 4 to 2 priority encoder is shown below.
| Inputs | Outputs | |||||
|---|---|---|---|---|---|---|
| Y3 | Y2 | Y1 | Y0 | A1 | A0 | V |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 0 | 1 | x | 0 | 1 | 1 |
| 0 | 1 | x | x | 1 | 0 | 1 |
| 1 | x | x | x | 1 | 1 | 1 |
Use 4 variable K-maps for getting simplified expressions for each output.
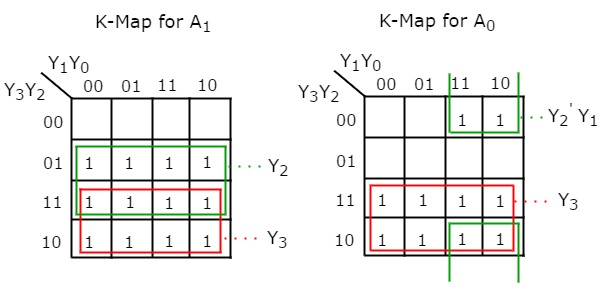
The simplified Boolean functions are
Similarly, we will get the Boolean function of output, V as
We can implement the above Boolean functions using logic gates. The circuit diagram of 4 to 2 priority encoder is shown in the following figure.
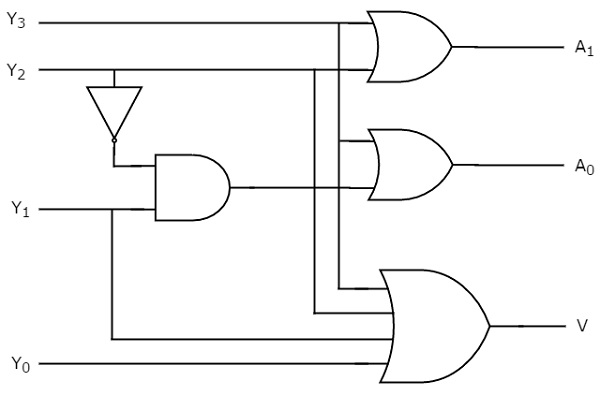
The above circuit diagram contains two 2-input OR gates, one 4-input OR gate, one 2input AND gate & an inverter. Here AND gate & inverter combination are used for producing a valid code at the outputs, even when multiple inputs are equal to ‘1’ at the same time. Hence, this circuit encodes the four inputs with two bits based on the priority assigned to each input.

Comments
Post a Comment